Mesh Topology Analysis using the Euler Characteristic
Within this small article, I am reviewing how the Euler formula for closed polyhedra can be used to efficiently analyze the topology of a 3D mesh, in order to detect its genus. This is useful in the context of some geometry processing applications, like UV unwrapping.
The Classical Euler Characteristic
The Euler characteristic (or Euler-Poincaré characteristic) is simply a number that we can compute for any closed polyhedron. Knowing the numbers of vertices, edges and faces, denoted as V/E/F, it is defined as
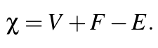
This number is always two for convex polyhedra, which is a very interesting and useful property. We'll come to more complicated cases later, for now let's just check the result for a simple example: a tetrahedron. The tetrahedron consists of four vertices, so V=4. It also consists of four faces, so F=4. Finally, there are three edges for the bottom triangle, plus another three originating at the bottom triangle's corners (all meeting at the tip), which makes six edges in total, so E=6. Plugging these numbers into the formula gives us V + F - E = 4 + 4 - 6 = 2. This is the expected result, and the same holds for all other convex polyhedra (if you are looking for a mathematical proof, there is a list of 20 different proofs by David Eppstein). This is a neat property - we can use the formula to compute the number of edges of a closed convex polyhedron, for instance, just by knowing the number of vertices and faces.
One can also show that retesselation or subdivision of the mesh does not change the result (the Euler characteristic). For example, when subdividing a quad into two triangles, we will add one more face, but also one more edge - that means F and E both become one larger, which means the differences cancel out in the formula above, so the result will remain the same. To give another example: If we perform an edge collapse on a triangle mesh, this operation will remove two triangles and one vertex, but also add three edges - the euler characteristic remains the same (the same holds for the inverse operation, a vertex split). Therefore, unless we really change the topology, the Euler characteristic of a manifold mesh doesn't change between a simple varaint and a high-resolution version obtained through vertex splits or subdivision methods.
Accounting for Boundaries
Knowing that the Euler characteristic works for convex polyhedra, it is interesting to check if we can actually apply it to more general 3D meshes. A first important aspect in this context are mesh boundaries, since most meshes that graphics applications are dealing with are not watertight. Especially for scenarios like UV unwrapping, where we need boundaries if we want to be able to unwrap a chart, it would be nice if we could still use the Euler characteristic to analyze the mesh topology. So let's take a look at the example image above that was used to illustrate the effect of an edge collapse. For simplicity, let's look at the simple mesh on the right hand side of that image, and let's imagine it would be a convex piece in 3D. The mesh consists of nine vertices (V=9), eight faces (F=8) and sixteeen edges (E=16). The euler characteristic for this mesh would therefore be 8+8-16=1... wait, that's strange. Wasn't the result supposed two? Well, actually, that only holds for closed, convex polyhedra, and this mesh isn't closed. Luckily, we can simply close it by adding one more face on the bottom:
Closing a hole to obtain a watertight convex polyhedron.
Having one more face, closing the boundary loop, the Euler characteristic is now two. In general, we can account for an arbitrary number of boundary loops this way: assuming they could each be replaced by a single, additional polygon, leading to a closed mesh, we can simply add the number of boundary loops B to the formula in order to support non-closed meshes, possibly with holes:
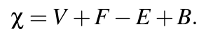
This also works for more complicated examples, of course, such as flat UV layouts with holes. A way to visualize this would be to fill all holes but the outer boundary and then unwrap the result using Tutte's or Floater's method, pinning the boundary to a circle. If we then smoothly pull up the center of the resulting mesh into the remaining dimension in 3D, we get a nice circular bottom that can be closed using one additional face, resulting in a closed, convex polyhedron. Here's an example:

A UV layout interpreted as a closed, convex 3D polyhedron with a Euler characteristic of two.
The 2D UV mesh of the cat model has a number V=372 vertices, F=662 faces and E=1035 edges. If we add B=3 to account for the boundary loops, we obtain 372 + 662 - 1035 + 3 = 2, which is the expected result for the closed, convex polhedron. This way of analyzing a mesh comes in handy if we want to check if we can actually unwrap a 3D mesh or not, as we will see in the next section.
Detecting the Genus
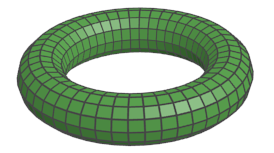
A torus: genus one, zero Euler characteristic.
Now, there are polyhedra which are not convex, and that applies to most real-world 3D meshes that we are dealing with in graphics. When computing the Euler characteristic for a certain kind of non-convex meshes, the result will be different from two. More specifically, the Euler characteristic is related to the genus of the 3D mesh. The genus is a topological measure telling us how many topological holes, or how many topological "handles" a 3D mesh has. The most simple example for a mesh with a topological hole / handle would be a donut, or, more formally speaking, a torus. As you can see on the example image, the torus has a topological hole (being "the middle of the ring", if you will). It therefore has a genus of one. At the same time, it doesn't have anything we would maybe otherwise call a "hole in the mesh": unlike the cat mesh that had holes in the surface, the 3D surface of the torus is still closed, or, in other words: it's still a watertight polyhedron.
For this kind of closed polyhedra with a nonzero genus, it has been shown that we can actually compute their genus (the number of topological holes / handles) from the Euler characteristic. Concretely speaking, the Euler characteristic will decreased by two for each topological hole. For the example of the torus, this means the Euler characteristic is not two, as it would be for convex closed polyhedra, but it is zero. Similarly, if we would have two topological holes (imagine something that is shaped like the number eight), the Euler characteristic would become minus two. Having a genus G, the following holds for all manifold meshes with boundary loops:

This is a very nice property, and we can actually use it to do useful things, such as detecting the genus of a mesh! Here's a simplified, watertight (B=0), and manifold version of the Stanford Happy Buddha mesh, consisting of a single connected component with V=24960 vertices, F=49940 faces and E=74910 edges, having six handles (G=6):
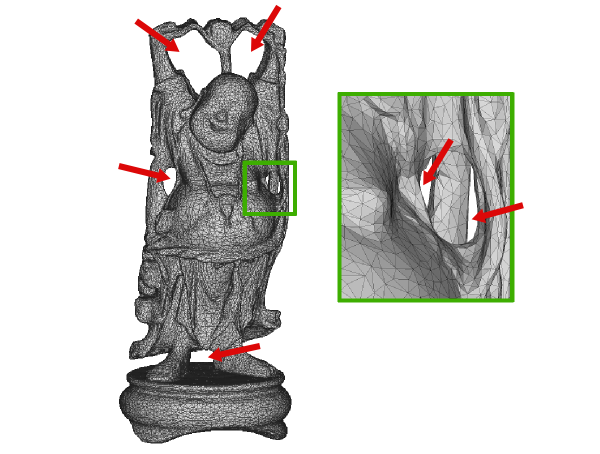
A large mesh with genus 6.
Plugging these values into the formula above results in 24960 + 49940 - 74910 + 0 = 2 - 2 * 6 = -10. The formula holds - pretty cool, isn't it? Exploiting this new knowledge, we can solve for G to compute the genus if we already have V, F, E and B!
In the context of UV mapping, having this possibility is pretty useful. We can, for example, efficiently check if a manifold mesh has one or more handles, which in turn tells us if the mesh can be unwrapped without any overlaps or not. Here are three examples of surface patches, where we can use the number of boundary loops B and the genus G (computed from V, F, E and B) in order to check if they have the right topology for unwrapping:
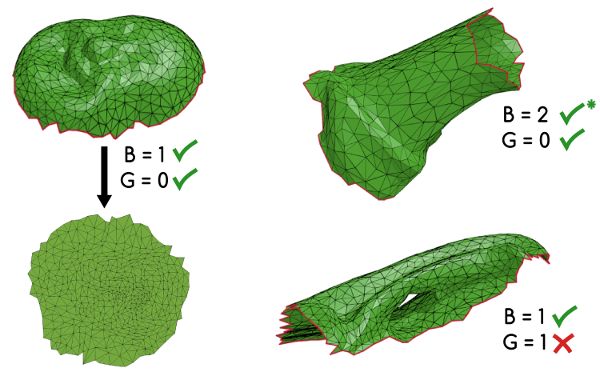
Checking if a 3D surface patch can be unwrapped. Required are at least one boundary loop and zero genus.
The patch on the left can be unwrapped, as it fulfills the requirements for "disc topology": a single boundary loop and zero genus. The patch on the upper right can be unwrapped as well, but depending on the algorithm to be used we may need to have exactly one boundary loop (disc topology), which we can obtain by temporarily filling one of the holes or, alternatively, by connecting them by a cut. The patch shown on the lower right can't be unwrapped, as it doesn't have zero genus (which could be fixed by introducing additional cuts). This is, of course, just a simple example, and there are probably many more interesting geometry processing applications where this kind of genus detection can be applied.
If you made it until here - congratulations ;-) I hope you liked my article - as always, if you have any feedback, corrections or additions that you would like to share with me, feel free to write me an email, or just comment in the respective twitter thread.
Other Articles